大林研究室は,
を募集しています。
岡山大学工学部数理データサイエンスコース以外の学生でも,数学・統計学・情報学・物理学などを勉強していて「数学的手法を活用したデータ解析」に興味がある学生,情報科学を勉強していて「トポロジーという数学にもとづくデータ解析手法の開発」に興味がある学生,また数学が専門で「位相的データ解析の数学」に興味がある学生,を歓迎します。 数理に重みを置くか手法に重みを置くか解析対象となる分野に重みを置くかは学生の興味と適正に基づいて決めます。
大林の分野は応用数学,特に位相的データ解析です。その他力学系や応用統計,マテリアルズインフォマティクスなどにも興味があります。
卒論:
修論:
進学希望者はまずは大林 (i.obayashi@okayama-u.ac.jp) まで連絡をください。 希望分野や研究計画について相談したいと思います。
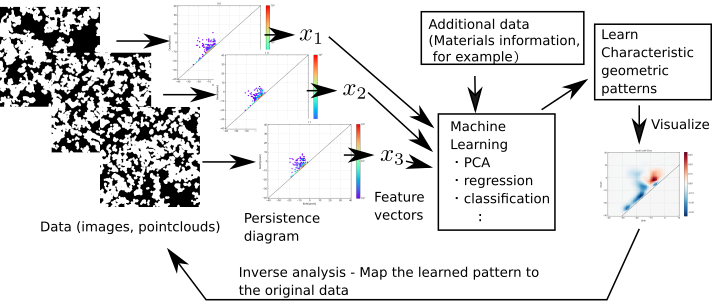
位相的データ解析とは数学のトポロジーを使ったデータ解析手法の総称で,複雑なデータの形を数学の力で定量化し,「形のデータサイエンス」を実現するための手法です。 材料科学,生命科学,画像処理など様々な方面で応用が今まさに進んでいる分野です。 大林は特にパーシステントホモロジーという手法の研究に取り組んでいます。
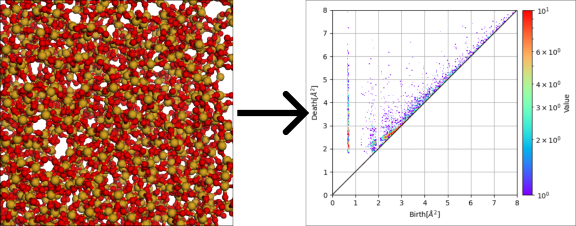
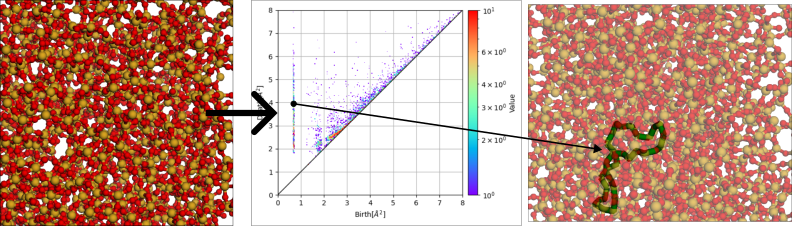
パーシステントホモロジーではデータから形の情報を縮約したパーシステンス図を計算し,この図を使ってデータの形の特徴を探索します。

このヒストグラムの各点が1がデータに含まれる孔やリング・空洞といった構造を表しています。
https://doi.org/10.1038/s43246-020-00100-3
金属ガラスは周期的な構造を持たない,乱れた原子配置を持つ金属です。 代表的な固体である結晶は三次元周期構造を持ち,その周期構造が様々な物性(物質の示す物理的性質)を決定します。 一方ガラスは周期的を持たず,乱れた構造を持っています。特に合金のガラスを金属ガラスと呼びます。 以下の図はパラジウムとケイ素の二元素からなる金属ガラスの原子配置です。

金属ガラスはこの乱れた構造が物性の鍵と考えられていますが,その構造をどのように特徴付けるべきかは決定的な方法がありません。 そこで,パーシステントホモロジーを使って構造を特徴付ける試みをしました。 パーシステントホモロジーで形を定量化し,機械学習を組み合わせてその背後にあるパターンを抽出することで特徴的なパターンを発見したのがこの研究です。
大林研究室ではパーシステントホモロジーに基くデータ解析ソフトウェア HomCloud を開発しています。 以下のような機能を持っています。
HomCloud は大林研究室の様々な研究,例えば材料科学への応用などに利用されています。
https://epubs.siam.org/doi/abs/10.1137/17M1159439 https://doi.org/10.1007/s41468-023-00119-8
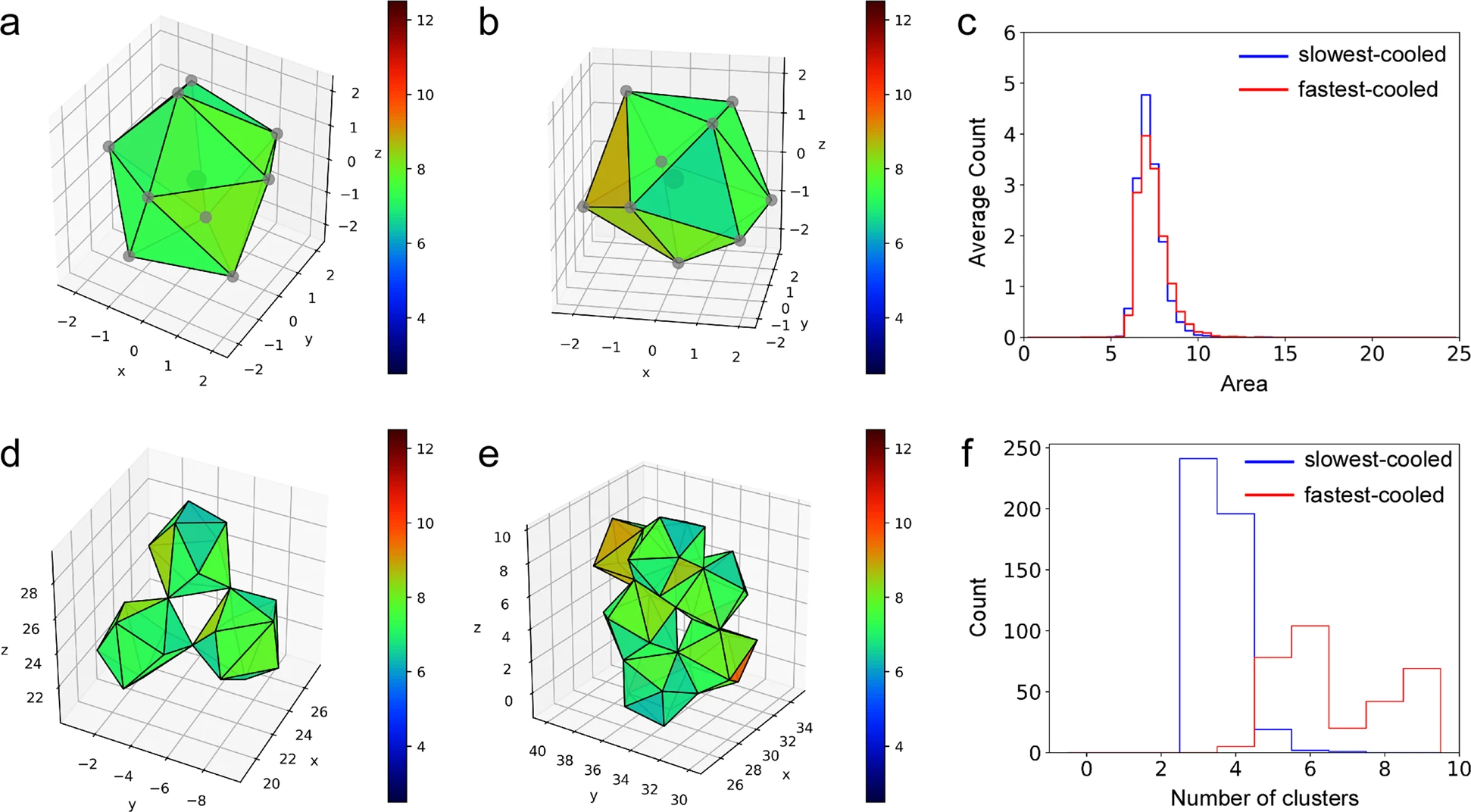
HomCloud の所で説明したように,パーシステントホモロジーによるデータ解析ではデータからパーシステンス図を計算し,この図からデータの幾何的特徴を読み解きます。 このとき,パーシステンス図が持っている幾何的情報が元データのどのような形に対応するかを特定するのが「逆解析」です。
パーシステンス図はデータの形の情報を圧縮するための手法なので,元データとは一対一に対応していません。 この対応を復元するためには工夫が必要で,この研究では線形計画法といった数理最適化の手法が用いられています。 数学と計算機科学の組み合わせによってこの手法が実現されているのです。
https://doi.org/10.1007/s41468-018-0013-5
パーシステントホモロジーはデータの形を定量的に特徴付けるための手法で,機械学習はデータの背後にあるパターンを抽出するための技法です。 そこでこの二つを組み合わせると,データの特徴的幾何パターンを抽出することができるようになります。 この研究ではパーシステンス図,パーシステントホモロジーの逆解析,そして線形モデルを組み合わせることで「解釈性の高い形の機械学習」が実現できることを示しています。
マテリアルズインフォマティクスは材料科学に情報学の手法を導入し,研究の効率化と新展開を目指す科学です。 材料科学(もっと広く物理学)では伝統的に実験,理論,計算機シミュレーションといった手法が用いられ研究が進められてきました。 そして,実験やシミュレーションのデータをより効果的に活用する「データ駆動的手法」の重要性が比較的古くから認識されていました。 そこで機械学習や計算機統計などの情報学の手法を導入していくという潮流がマテリアルズインフォマティクスです。
上で挙げたパーシステントホモロジーによる金属ガラスの解析などもマテリアルズインフォマティクスの一例と捉えることができます。 大林は応用数学の専門家としてこういったマテリアルズインフォマティクスの問題にも取り組んでいます。
https://doi.org/10.1107/S1600576724010872
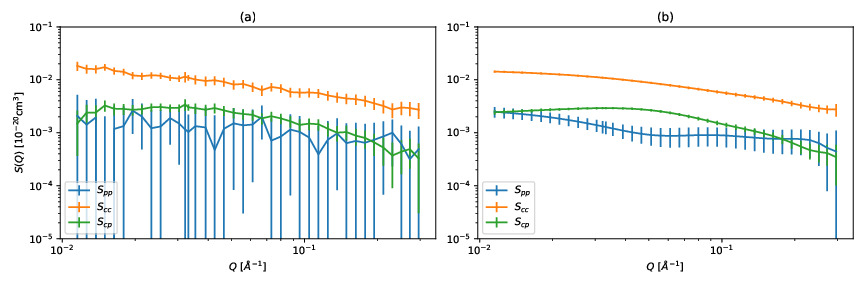
この研究ではコントラスト変調中性子小角散乱実験のデータから部分散乱関数を高精度かつ効率的に推定する手法を提案したものです。 この実験は中性子を試料に照射して散乱強度を測定し,物質のナノ構造を解析する手法です。 水素の一部を重水素に置き換えた複数試料を用いることで,多成分系の構造情報を成分ごとに抽出可能となる強力な手法です。 試料のミクロ構造情報から部分散乱関数が決まり,部分散乱関数から散乱強度が決まるため,これを散乱強度から逆向きに推定することで構造を推定することができます。 中性子実験は実験が大変でコストが高いため,できるだけ少ない照射時間で精度の高い推定ができる手法が必要とされています。
この研究ではガウス過程回帰と呼ばれるベイズ推定の一種を利用し,部分散乱関数を高精度に推定する手法を開発しました。
大学院生の研究課題としては,以下のようなものが挙げられます。 もちろんこれらに限定されるものではありませんが,あまりかけ離れていると大林が指導するのが難しくなります。
これらのトピックは大林のこれまでの研究と関連するものや,今後の研究の方向性と関連しているトピックです。
以下のようなトピックが考えられます。
材料科学や細胞のデータなどは大林が共同研究者に依頼して収集することができますが,それ以外のデータをやりたい場合は自分でデータを探してくる必要があります。
この分野は数理(線形代数,微積,統計,基本的な機械学習など)とプログラミング(Pythonを使います)がバランス良くできる学生が向いています。
また,解析対象となるデータに関する知見があると非常に有用です。 専門が材料科学の場合は,材料科学の研究室に所属して大林の研究室と共同研究する,という体制も良いでしょう。そちらの研究室の教員とも相談してください。
上で挙げた原子配置データや材料科学画像の解析などに加え,中性子小角散乱データの解析手法開発といったトピックがあります。 こちらは眞弓先生 (東大物性研) との共同研究です。
眞弓先生が得意としている散乱実験であるコントラスト変調中性子小角散乱は,試料の重水素化率を変化させることで成分ごとの中性子散乱強度を変化させ,多成分系の構造を推定可能な手法です。 最終的に知りたい構造の情報(例えば球形の分子の半径など)と実験データとの間には複雑な物理モデルがあり,実験データから構造を推定するにはこれらの物理モデルを適切に統計モデルとして表現し,その推定方法を改善する方法を開発します。
この分野も数理と計算機がバランス良くできる学生が向いています。特にベイズ推定を勉強しておくとよいでしょう。
パーシステントホモロジーを利用した解析手法開発は大林の重要なトピックです。例として以下のような研究内容を想定しています。
この分野(数学アルゴリズムなど)に関しては,数学と情報科学の両方でそれなりに高度な知識が必要です。 「数学アルゴリズム」はブルーオーシャンな分野が結構あって位相的データ解析もその一つだと思いますが,数学と情報科学の2つの道具を駆使する必要があります。
数理データサイエンスコースの学生にはお勧めしませんが,理学部数学科で数学の勉強をしてきた学生であればパーシステントホモロジーの理論研究も指導可能なトピックの一つです。 大林研究室でやるのであれば計算機での実装可能性も重視したいのでハードルが高い(数学と計算機を両方勉強してきて欲しい)ですが,こういった挑戦的な問題に取り組む学生を歓迎します。
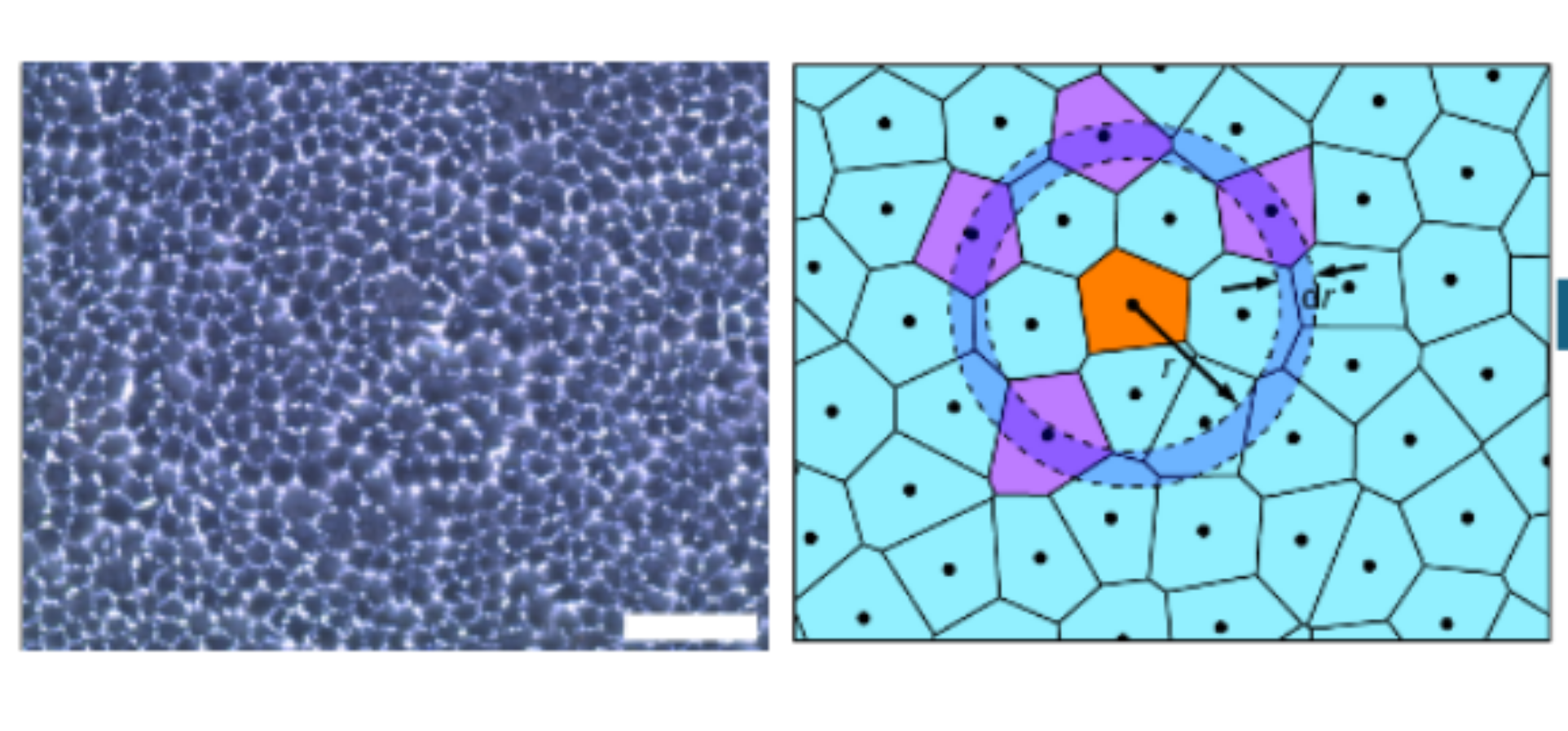
大林研究室では材料科学データのデータ解析をよく行っています。 このようなマテリアルのデータを研究対象とする利点には以下のようなものがあり,材料科学データ解析はお勧めするトピックの一つです。
以上のようなトピックについて研究をしたい場合は,以下のような内容を勉強する必要があります。
これ以外でも,以下のような知識があると研究に有利です。
手前味噌ですが,パーシステントホモロジーに関しては大林も執筆に参加した以下の教科書がお勧めです。
岡山大学大学院環境生命自然科学研究科は岡山大学の理・工・農学の多くの分野を統合した研究科です。 大林研究室に進学する学生はこの研究科に所属します。
募集要項は以下の通りです。
この研究科は,学位プログラム / コース / 研究分野 / 指導教員という4段階で構成されていて,各学生はこれらを選択します。大学院のシステムは組織変更のため階層が多くなっています。大林研究室の場合
という階層になっています。
博士前期課程は2年でコースワーク(授業)と指導教員の指導による研究を行い,必要な単位を取得し最終的に修士論文の執筆と研究発表を実施することで修士の学位が認められます。 数理データ科学コースの提供する授業を中心に受講します。 数理情報科学学位プログラムの提供する授業であれば幅広く取ることもできます。 つまり数理データ科学コースの授業の他に数学や情報科学のコースの授業なども取ることができます。 また,企業や官公庁へのインターンシップ,学会発表などによる単位取得が修了条件に含まれます。
博士後期課程は3年間の研究を博士論文にまとめることで博士の学位が認められます。 博士後期課程は研究者養成課程であって,その学位は研究者として最低限の能力があることを証明するものなので,学術雑誌への論文の執筆,投稿,査読者とのやりとり,学術講演,といった研究者としての一通りの活動を経験する必要があります。 そのためこれらの経験も学位の条件として設定されています。